1.荷重倍数の計算
巡行時において、機体にかかる揚力と重力は釣合を保っているが、引き起こし時には揚力が重力を上回るようになる。強度計算において、この揚力の変化は無視できない。
そこで、揚力と重力との比を荷重倍数と定義して用いることにする。荷重倍数nは引き起こし終了時の最低高度において、最大である。機体重量をW、速度をVとすると、垂直方向の力の釣合を考えて、
L = W + WV^2/gr
荷重倍数nは
n = L/W = 1 + V^2/gr
引き起こし速度を半経験的に8.24[m/s]として、
引き起こし半径r[m] 荷重倍数n
8 1.866
6 2.155
となり、引き起こし半径は6[m]が限界であり、荷重倍数の最大値nmaxは
nmax=2.155
として考えることにする。
2.主翼の捻りに対する対策
主翼の強度計算において、捻りは最も重要であるといっても過言ではない。私達の機体の主翼は主桁を翼型の風圧中心に通しているので、水平巡行時において捻りモーメントは発生しない。しかし、水平下降時での進行方向への力の発生により、捻りモーメントは誘起されてしまい、さらに製作精度を考えると水平巡行時においても捻りモーメントはゼロであるとはいい難く、捻りに対する何らかの対策を講じなければならないと考え、主翼にはリヤスパーが取り付けられている。
3.主翼の強度計算
今年の主翼の桁は全部で7本のカーボンパイプにより構成する奇数翼とし、昨年の機体である「たんせい伍号」のものを継続して使用する。パイプのスペックは以下の通りである。
| 中央翼 | 内翼 | 外翼 | 最外翼 | |
| 長さ [mm] | 1800 | 4300 | 4300 | 4200 |
| 内径(root) [mm] | 70 | 75.4 | 70 | 55 |
| (tip) [mm] | 70 | 67 | 50 | 37 |
| 肉厚 [mm] | 2.0 | 1.0 | 1.0 | 0.6 |
| 繊維 | HR40 | HR40 | HR40 | HR40 |
| 本数 | 1 | 2 | 2 | 2 |
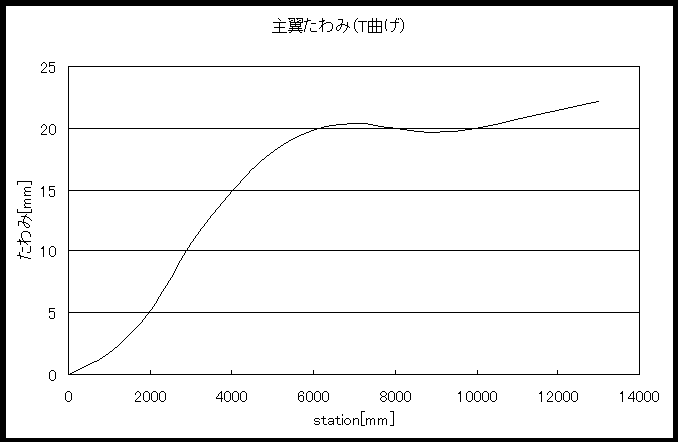
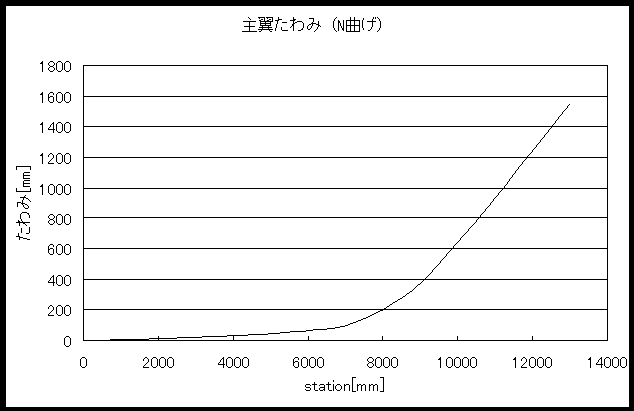
桁同士の結合重複部分はすべて200[mm]としてつなぎ合わせる。また、主翼の中央から7.6[m]の位置に張線を張る。強度計算は、主翼のスパン方向のCl分布、重量分布を考慮して、有限要素法により主翼のたわみを計算し、強度を確認する。その結果、水平飛行時の主翼の垂直方向のたわみは翼端で1.57[m] となった。また、水平下降時にかかる進行方向への力に対して強度を持たせるために主翼にリヤスパーを取り付けることとし、リヤスパーを下図のように設計した。
有限要素法により計算して、主翼の進行方向のたわみは2.27[cm] となった。両者のたわみ曲線と水平飛行時の主翼のBMDをこの章の最後に添付する。
グラフより、曲げモーメントMは翼の中央部から7.5[m]の所で最大となり、さらに、有限要素法により計算して、軸圧縮力Nも最大となっているから、この時、圧縮応力σは、
σ=0.5 M×D/I+N/A=15.88[kgf/mm2]=155.6[MPa]
ただし、I:断面二次モーメント、A:断面積、D:外経とする。
荷重倍数をn=2.155として、
σ=155.6×2.155=335.3[MPa]<400[MPa](許容応力)
となるので、主翼の強度は十分であるといえる。
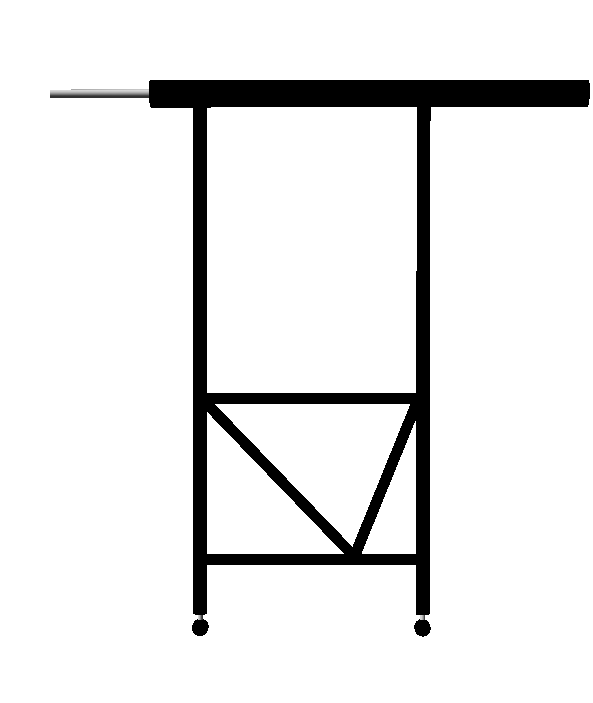
4.コックピットの強度計算
今年のコックピットは、部材にカーボンをパイプを使用する。コックピットの仕様を図に示すと次のようになる。
さて、このコックピットには、地面からの垂直抗力を受けるので、引き起こし時ではなく地上静止時において一番大きい荷重がかかる。有限要素法により計算すると、コックピット前方の主翼と結合している部分に一番大きな力がかかり、そのとき、
安全率S = 4.33
となり、強度は十分であるといえる。