[latexpage]
6.1 主翼
6.1.1 主翼面積の決定
機体重量 W = 100 (kgf)
空気密度 ρ = 0.119 (kgf・s^2 / m^4)
揚力係数 CL = 1.1
上半角 Γ = 10゜
として次式から主翼面積を決定する。
begin{equation}
ScosGamma = frac{2W}{rho C_L V^2}
end{equation}
若干の余裕をみて主翼面積 S = 28.0 (m^2) として製作することにする。
6.1.2 主翼平面形の決定
主翼の平面形は以下の事項を考慮して決定する必要がある。
(1)循環分布ができるだけ楕円分布に近い
誘導抵抗係数は次式で表される。
begin{equation}
C_{D_i} = frac{{C_L}^2}{pi e AR}
end{equation}
飛行効率eは循環分布が楕円分布のときに最大値 e = 1 をとり、楕円分布からずれると e < 1 となる。したがって、循環分布はできるだけ楕円分布に近いことが望ましい。
(2)翼端失速が起こりにくい
翼端失速というのは、断面揚力係数Clが翼の途中で最大値を取ると、迎角が増えたときにそこから失速が始まるというものである。翼端失速が生じるとロール安定が損なわれてしまう。翼端失速を生じさせないために、Clの最大値がなるべく翼根に来るように設計する。
(3)翼端にかけて荷重を減らす
主翼構造の問題で、荷重を持ってくると翼根での曲げモーメントが大きくなってしまうためである。この問題は、テーパをつけることで回避する。
(4)製作が容易であること
設計を確実に実現するために重要な要素である。具体的には直線的なテーパ、捩り下げなし等が挙げられる。
6.1.3 主翼平面形の最適化
上述した(1)を実現するために、主翼接合部ごとのコード長を変化させながら、循環の楕円分布とのずれが最小となる平面形を求めるプログラムを作成した。
循環は断面揚力係数Cl 、翼弦長c、機速Vとして次式で表される。
begin{equation}
Gamma = frac{1}{2}C_l cV
end{equation}
断面揚力係数Clの計算には以下に示すシュレンクの近似式を用いた。
begin{equation}
C_l = frac{C_{l_alpha}}{2}left(alpha_{w0} – frac{2epsilon_t}{b}yright)+frac{1}{2}left(1+frac{4S}{pi bc}sqrt{1-(frac{2y}{b})^2}right)C_L
end{equation}
Clα : 揚力傾斜
εt : 捩り下げ
b : スパン長
y : 翼根からの距離
αw0 : rootの翼基準線からのzero liftの角度
今年の設計ではεt = 0゜としたので結局、
begin{equation}
Gamma = frac{1}{4} left( 1+frac{4S}{pi bc} sqrt{1-(frac{2y}{b})^2} right) cVC_L
end{equation}
となる。 また、目指す循環分布は
begin{equation}
Gamma_{opt} = Gamma^ast sqrt{1-(frac{2y}{b})^2}
end{equation}
で定める。ただし、Γ*は揚力の拘束条件から以下の式を満たすように決定する。
begin{eqnarray}
L &=& 2int_0^{b/2} frac{1}{2}rho cV^2 C_l dy \
C_l &=& frac{2Gamma^ast}{cV}sqrt{1-(frac{2y}{b})^2} \
L &=& W
end{eqnarray}
各接合部ごとのコード長を翼面積一定の拘束条件の元で変化させながら楕円分布からのずれを表す評価関数Zが最小になる平面形を求める。ここで評価関数Zは以下のように定義する。
begin{equation}
Z = int_0^{b/2} (Gamma – Gamma_{opt})^2 dy
end{equation}
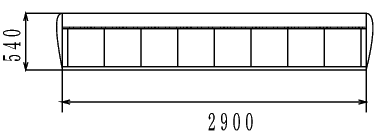
製作の関係上、y = 5700 (mm)の接合部からテーパを開始することとし、平面形は以下のように決定した。
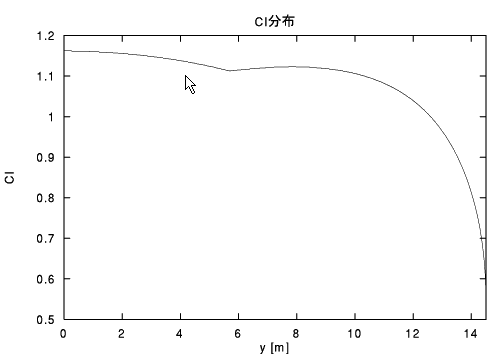
6.1.4 断面揚力係数分布
これまで求めた数値を用いて断面揚力係数Clの分布を求めると次のようになる。グラフからも分かるようにClの最大値は翼根にきており、翼端失速の危険性は少ないと考えられる。
6.1.5 主桁位置の決定
風圧中心位置は次式より求まる。
C.P. = 0.25 – CM / CL
CM 、CL値をデータから読みとって代入すると、
α = 4゜ : C.P. = 0.25 – (-0.129) / 1.1 = 0.367
α = 6゜ : C.P. = 0.25 – (-0.130) / 1.31 = 0.349
α = 8゜ : C.P. = 0.25 – (-0.128) / 1.50 = 0.355
迎角が大きいときでも捩り上げが起こりにくくするために、主桁位置は33%とする。
6.2 水平尾翼
6.2.1 面積
水平尾翼容積は次のように表される。
begin{equation}
V_h =S_h l_h/(bar{c}S)
end{equation}
lh : テールモーメントアーム
Sh : 水平尾翼面積
S : 主翼面積
c : 主翼平均空力翼弦
過去の機体のデータからVh=0.3と決定した。テールモーメントアームlh5.3(m)として Sh=1.57(m2)
6.2.2 平面形
スパン2.9(m)の矩形翼とする。
6.2.3 安定性
以上の値より縦の静安定を示すCmαを求める。
Cmα=-1.98
Cmαの値が負になっているので、迎角静安定を有する。
6.3 垂直尾翼
6.3.1 面積
垂直尾翼容積は次のように表される。
begin{equation}
V_v =S_v l_v/(bS)
end{equation}
lv : テールモーメントアーム
Sv : 垂直尾翼面積
S : 主翼面積
b : 主翼スパン
1996年度の大会でみられたスパイラルモードの不安定性を改善するために、昨年度の機体ではVv=0.010であった。今回もこの値を採用し、lv=6.1(m)として Sv=1.33(m^2)
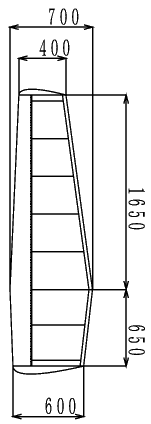
6.3.2 平面形
昨年度の機体よりも主翼スパンを延長したために、垂直尾翼取り付け位置が後退する結果となった。離陸時に垂直尾翼下部がプラットホームに接触しないように、垂直尾翼下部を短くする。
6.4 抵抗推算
全機抵抗CDは、有害抵抗係数CD0、誘導抵抗係数CDiを用いて次式で表される。
CD = CD0 + CDi
6.4.1 有害抵抗係数の推算
各部分の抵抗係数を定義する基準面積をSπとし、Sπを用いたときの抵抗係数をCDπとすると、
begin{equation}
C_{D_0} = (1+k) frac{sum C_{D_pi} cdot S_pi }{S}
end{equation}
kは干渉等に対する補正係数で、今回はk = 0.1とする。以下にSπとCDπの関係を示す。
| Sπ(m2) | CDπ | |
| 主翼 | 28.0 | 0.001 + CDω |
| 水平尾翼 | 1.566 | 0.008 |
| 垂直尾翼 | 1.33 | 0.008 |
| 胴体 | 0.0078 | 0.1 |
| フェアリング | 1.26 | 0.1 |
| キングポスト | 0.05 | 0.1 |
| ワイヤー | 0.06 | 1.5 |
DAE11の場合、CL=1.1のとき、主翼抵抗係数CDω=0.0095であるから、
CD = 0.02117
となる。
6.4.2 誘導抵抗係数の推算
誘導抵抗係数CDiは次式で与えられる。
begin{equation}
C_{D_i} = frac{{C_L}^2}{e pi AR_{eh}}
end{equation}
ただし、eは飛行機効率、ARehは地面効果を考慮したアスペクト比で次のように表される。
begin{equation}
AR_{eh} = frac{1 + 33 (h/b)^{1.5}}{33 (h/b)^{1.5}} cdot AR
end{equation}
e = 0.9としてAR = 30、b = 29 (m^2)、CL = 1.1を代入すると、次のようになる。
| 高度h(m) | AReh | 誘導抵抗係数CDi |
| 10 | 34.49 | 0.0124 |
| 9 | 35.26 | 0.0121 |
| 8 | 36.27 | 0.0118 |
| 7 | 37.67 | 0.0114 |
| 6 | 39.66 | 0.0108 |
| 5 | 42.70 | 0.0100 |
| 4 | 47.75 | 0.0090 |
| 3 | 57.32 | 0.0075 |
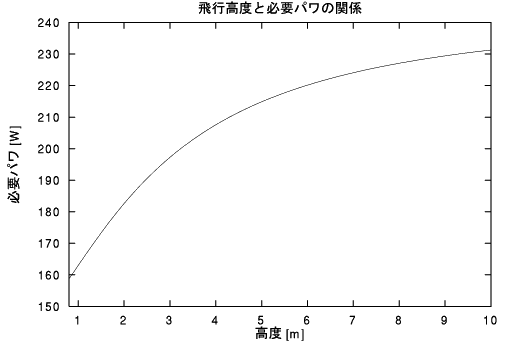
6.5 必要パワ
推力をT、抵抗をD、機速をv、必要パワをPとすると、
begin{equation}
P = Tv = Dv = frac{1}{2}rho v^2 SC_D cdot v = frac{1}{2} rho v^3 S(C_{D_0}+C_{D_i})
end{equation}
飛行高度と必要パワの関係を下図に示す。